Условия перпендикулярности двух прямых в пространстве. Параллельные прямые, признаки и условия параллельности прямых

УГОЛ МЕЖДУ ПЛОСКОСТЯМИ

Рассмотрим две плоскости α 1 и α 2 , заданные соответственно уравнениями:

Под углом между двумя плоскостями будем понимать один из двугранных углов, образованных этими плоскостями. Очевидно, что угол между нормальными векторами и плоскостей α 1 и α 2 равен одному из указанных смежных двугранных углов или . Поэтому . Т.к. и , то

Пример. Определить угол между плоскостями x +2y -3z +4=0 и 2x +3y +z +8=0.

Условие параллельности двух плоскостей.

Две плоскости α 1 и α 2 параллельны тогда и только тогда, когда их нормальные векторы и параллельны, а значит .

Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:

или

Условие перпендикулярности плоскостей.

Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, или .

Таким образом, .

Примеры.

ПРЯМАЯ В ПРОСТРАНСТВЕ.

ВЕКТОРНОЕ УРАВНЕНИЕ ПРЯМОЙ.

ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ

Положение прямой в пространстве вполне определяется заданием какой-либо её фиксированной точки М 1 и вектора , параллельного этой прямой.

Вектор , параллельный прямой, называется направляющим вектором этой прямой.

Итак, пусть прямая l проходит через точку М 1 (x 1 , y 1 , z 1), лежащую на прямой параллельно вектору .

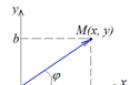
Рассмотрим произвольную точку М(x,y,z) на прямой. Из рисунка видно, что .

Векторы и коллинеарны, поэтому найдётся такое число t , что , где множитель t может принимать любое числовое значение в зависимости от положения точки M на прямой. Множитель t называется параметром. Обозначив радиус-векторы точек М 1 и М соответственно через и , получаем . Это уравнение называется векторным уравнением прямой. Оно показывает, что каждому значению параметра t соответствует радиус-вектор некоторой точки М , лежащей на прямой.

Запишем это уравнение в координатной форме. Заметим, что , и отсюда

Полученные уравнения называются параметрическими уравнениями прямой.

При изменении параметра t изменяются координаты x , y и z и точка М перемещается по прямой.

КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ

Пусть М 1 (x 1 , y 1 , z 1) – точка, лежащая на прямой l , и – её направляющий вектор. Вновь возьмём на прямой произвольную точку М(x,y,z) и рассмотрим вектор .

Ясно, что векторы и коллинеарные, поэтому их соответствующие координаты должны быть пропорциональны, следовательно,

– канонические уравнения прямой.

Замечание 1. Заметим, что канонические уравнения прямой можно было получить из параметрических,исключив параметр t . Действительно, из параметрических уравнений получаем или .

Пример. Записать уравнение прямой в параметрическом виде.

Обозначим , отсюда x = 2 + 3t , y = –1 + 2t , z = 1 –t .

Замечание 2. Пусть прямая перпендикулярна одной из координатных осей, например оси Ox . Тогда направляющий вектор прямой перпендикулярен Ox , следовательно, m =0. Следовательно, параметрические уравнения прямой примут вид

Исключая из уравнений параметр t , получим уравнения прямой в виде

Однако и в этом случае условимся формально записывать канонические уравнения прямой в виде. Таким образом, еслив знаменателе одной из дробей стоит нуль, то это означает, что прямая перпендикулярна соответствующей координатной оси.

Аналогично, каноническим уравнениям соответствует прямая перпендикулярная осям Ox и Oy или параллельная оси Oz .

Примеры.

ОБЩИЕ УРАВНЕНИЯ ПРЯМОЙ, КАК ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ПЛОСКОСТЕЙ

Через каждую прямую в пространстве проходит бесчисленное множество плоскостей. Любые две из них, пересекаясь, определяют ее в пространстве. Следовательно, уравнения любых двух таких плоскостей, рассматриваемые совместно представляют собой уравнения этой прямой.

Вообще любые две не параллельные плоскости, заданные общими уравнениями

определяют прямую их пересечения. Эти уравнения называются общими уравнениями прямой.

Примеры.

Построить прямую, заданную уравнениями

Для построения прямой достаточно найти любые две ее точки. Проще всего выбрать точки пересечения прямой с координатными плоскостями. Например, точку пересечения с плоскостью xOy получим из уравнений прямой, полагая z = 0:

Решив эту систему, найдем точку M 1 (1;2;0).

Аналогично, полагая y = 0, получим точку пересечения прямой с плоскостью xOz :

От общих уравнений прямой можно перейтик её каноническим или параметрическим уравнениям. Для этого нужно найти какую-либо точку М 1 на прямой и направляющий вектор прямой.

Координаты точки М 1 получим из данной системы уравнений, придав одной из координат произвольное значение. Для отыскания направляющего вектора, заметим, что этот вектор должен быть перпендикулярен к обоим нормальным векторам и . Поэтому за направляющий вектор прямой l можно взять векторное произведение нормальных векторов:

Пример. Привести общие уравнения прямой к каноническому виду.

Найдём точку, лежащую на прямой. Для этого выберем произвольно одну из координат, например, y = 0 и решим систему уравнений:

Нормальные векторы плоскостей, определяющих прямую имеют координаты Поэтому направляющий вектор прямой будет

. Следовательно, l : .

УГОЛ МЕЖДУ ПРЯМЫМИ

Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.

Пусть в пространстве заданы две прямые:

Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами и . Так как , то по формуле для косинуса угла между векторами получим

Глава V*. Уравнения прямых и плокостей в пространстве.

§ 70. Условия параллельности и перпендикулярности двух прямых.

Прямые с направляющими векторами а и b :

а) параллельны тогда и только тогда, когда векторы а и b коллинеарны;

б) перпендикулярны тогда и только тогда, когда векторы а и b перпендикулярны, т. е. когда а b = 0.

Отсюда получаем необходимые и достаточные условия параллельности и перпендикулярности двух прямых, заданных каноническими уравнениями.

Для того чтобы прямые

были параллельны, необходимо и достаточно чтобы выполнялось условие

В случае, если какое-либо из чисел b 1 , b 2 , b 3 равно нулю, то должно обращаться в нуль соответствующее ему число a 1 , a 2 , a 3 .

Для перпендикулярности прямых необходимо и достаточно, чтобы выполнялось условие

a 1 b 1 + a 2 b 2 + a 3 b 3 = 0. (2)

Задача 1. Среди следующих пар прямых указать пары параллельных или перпендикулярных прямых:

а) Направляющие векторы a = (2; 4; -13) и b = (3; 5; 2) очевидно, не коллинеарны. Следовательно, прямые не параллельны. Проверим условие перпендикулярности

a 1 b 1 + a 2 b 2 + a 3 b 3 = 2 3 + 4 5 - 13 2 = 0.

Прямые перпендикулярны.

б) Направляющий вектор второй прямой имеет координаты b = (3; 2; 4). За направляющий вектор первой примой можно взять векторное произведение нормальных векторов
n 1 = (2; -3; 0) и n 2 = (4; -2; -2) плоскостей, задающих эту прямую:

Условие (1) выполняется, так как 6 / 3 = 4 / 2 = 8 / 4 . Прямые параллельны.

в) Направляющий вектор первой прямой имеет координаты а = (2; 3; 1). Уравнения второй прямой легко приводятся к каноническому виду

Следовательно, b =(- 1 / 2 ; 1; 3 / 2) .

Векторы а и b не параллельны. Они и не перпендикулярны, так как

a 1 b 1 + a 2 b 2 + a 3 b 3 = 2 (- 1 / 2) + 3 + 3 / 2 =/= 0.

Данные прямые не параллельны и не перпендикулярны.

Задача 2. Найти уравнение прямой, проходящей через точку М 0 (2; -3; 4) перпендикулярно прямым

Лекция 8. Условия параллельности и перпендикулярности прямых. Прямая и плоскость в пространстве

Взаимное расположение прямых на плоскости;

Уравнение плоскости в пространстве;

Прямая в пространстве;

Примеры решения задач.

8.1. Взаимное расположение прямых на плоскости

Угол между двумя прямыми. Пусть заданы две прямые на плоскости: (1) и
(2) и требуется определить угол между ними (см. рис. 8.1).

Рис. 8.1. Угол между двумя прямыми

Из рис. 8.1. видно, что
, причем
и
,
.

Тогда
или

. (8.1)

Условия параллельности и перпендикулярности прямых.

Пусть заданы две прямые:

(1);

(2).

Прямые (1) и (2) параллельны тогда и только тогда, когда
.

Если прямые перпендикулярны, то
и .

тогда и только тогда, когда
.

Пусть прямые заданы общими уравнениями:

(1);

(2).

В этом случае угловые коэффициенты
и
и условие параллельности примет вид:

Прямые (1) и (2) параллельны тогда и только тогда, когда
.

Следовательно, условием параллельности прямых, заданных общими уравнениями, является пропорциональность коэффициентов при переменных.

Условием перпендикулярности двух прямых, заданных общими уравнениями, является равенство нулю суммы произведений коэффициентов при переменных и .

Действительно, т.к.
, то
.

Прямые (1) и (2) перпендикулярны тогда и только тогда, когда
.

Точка пересечения прямых.

Пусть прямые заданы общими уравнениями:
и
.

Так как координаты точки пересечения должны удовлетворять каждому из уравнений, то их можно найти из системы:

Расстояние от точки до прямой.

Пусть даны точка
и прямая
.

Рис. 8.2. Расстояние от точки до прямой

Под расстоянием от точки до прямой понимается длина перпендикуляра
, опущенного из точки
на прямую (рис. 8.2).

Для нахождения расстояния необходимо:

В итоге получается формула:

. (8.2)

8.2. Уравнение плоскости в пространстве

а) Задание плоскости по точке и нормальному вектору. Пусть плоскость проходит через точку
перпендикулярно вектору
(рис.8.3).

Рис. 8.3. Плоскость, заданная точкой и нормальным вектором

Вектор
называется нормальным вектором плоскости .

Возьмем в плоскости произвольную точку
. Тогда вектор будет перпендикулярен вектору
. Значит скалярное произведение этих векторов равно нулю, т.е. в координатном виде:

Уравнение плоскости можно записать в виде:

где
.

Уравнение (8.4) называется общим уравнением плоскости.

б) Задание плоскости по трем точкам. Возьмем на плоскости три точки, не лежащие на одной прямой:
,
,
.

Рис. 8.4. Задание плоскости по трем точкам

Зададим векторы и . Так как три данные точки не лежат на одной прямой, то заданные векторы не коллинеарные (не параллельны и не лежат на одной прямой). Векторы
и
образуют базис двумерного пространства.

В плоскости возьмем произвольную точку
. Зададим вектор . Так как векторы
и
образуют базис, то вектор
является линейной комбинацией базисных векторов. Значит, строки матрицы, составленной из координат этих векторов, линейно зависимы и определитель такой матрицы равен нулю:

. (8.5)

в) Задание плоскости по точке
, лежащей на плоскости и двум направляющим векторам (векторы лежат в данной плоскости или параллельны плоскости)
и
.

Рассуждения аналогичны рассуждениям под буквой б), поэтому получим:

. (8.6)

Частные случаи общего уравнения плоскости :

Если
, то уравнение
определяет плоскость, проходящую через начало координат.

Если
, то уравнение
определяет плоскость, параллельную
. Аналогично при
параллельность
и при
параллельность
.

Если
, то
определяет плоскость, параллельную плоскости
. При
параллельность
, при
параллельность
.

Если
, то
определяет плоскость, проходящую через ось
. При
проходит через
, при
проходит через
.

Если
, то
определяет координатную плоскость
. При
плоскость
, при
плоскость
.

Условия параллельности и перпендикулярности плоскостей определяются условиями коллинеарности и перпендикулярности нормальных векторов
и
.

Условием параллельности двух плоскостей является пропорциональность коэффициентов при одноименных переменных:

Условие перпендикулярности:

а) Прямая в пространстве может быть задана, как линия пересечения двух плоскостей:

б) Если прямая параллельна вектору
(направляющий вектор) и проходит через точку
, то из условия коллинеарности векторов и
(где
- произвольная точка прямой) получим:

. (8.7)

Уравнения (8.7) называются каноническими уравнениями прямой линии в пространстве.

в) Уравнения (8.7) можно записать в параметрическом виде:

;

Приравнивая каждую дробь к параметру
, получим:

(8.8)

Уравнения (8.8) называются параметрическими уравнениями прямой в пространстве.

8.4. Примеры решения задач

Пример 1. Составить уравнение прямой, проходящей через точку
:

а) параллельно прямой :
;

б) перпендикулярно прямой :
.

Решение.

а) Так как искомая прямая параллельна прямой :
, то
. Найдем исходной прямой
. Откуда получим, что
.

Итак, искомую прямую задаем по точке
и угловому коэффициенту
:

б) Так как искомая прямая перпендикулярна прямой :
, то
. Из уравнения исходной прямой получаем
. Тогда
.

Уравнение искомой прямой:

Ответ: а)
; б)
.

Пример 2. Составить уравнение плоскости , проходящей через точку
и:

а) параллельной плоскости :
;

б) точку
, параллельной оси
;

в) проходящей через ось
.

Решение.

а) Так как искомая плоскость параллельна плоскости
, то нормальный вектор последней плоскости будет нормальным вектором и для искомой плоскости. Значит,
и для задания уравнения используем формулу (8.3):

б) Так как плоскость параллельна
, то в общем уравнении (8.4) коэффициент
, и уравнение имеет вид
. Так как точки
и
лежат на плоскости, то их координаты должны удовлетворять уравнению плоскости:

Следовательно, уравнение плоскости имеет вид:

в) Так как плоскость проходит через ось
, то
, т.е. уравнение плоскости имеет вид
. Так как плоскость содержит точку
, то . Уравнение плоскости запишется:

Ответ: а)
; б)
; в)
.

Эта статья о параллельных прямых и о параллельности прямых. Сначала дано определение параллельных прямых на плоскости и в пространстве, введены обозначения, приведены примеры и графические иллюстрации параллельных прямых. Далее разобраны признаки и условия параллельности прямых. В заключении показаны решения характерных задач на доказательство параллельности прямых, которые заданы некоторыми уравнениями прямой в прямоугольной системе координат на плоскости и в трехмерном пространстве.

Навигация по странице.

Параллельные прямые – основные сведения.

Определение.

Две прямые на плоскости называются параллельными , если они не имеют общих точек.

Определение.

Две прямые в трехмерном пространстве называются параллельными , если они лежат в одной плоскости и не имеют общих точек.

Обратите внимание, что оговорка «если они лежат в одной плоскости» в определении параллельных прямых в пространстве очень важна. Поясним этот момент: две прямые в трехмерном пространстве, которые не имеют общих точек и не лежат в одной плоскости не являются параллельными, а являются скрещивающимися.

Приведем несколько примеров параллельных прямых. Противоположные края тетрадного листа лежат на параллельных прямых. Прямые, по которым плоскость стены дома пересекает плоскости потолка и пола, являются параллельными. Железнодорожные рельсы на ровной местности также можно рассматривать как параллельные прямые.

Для обозначения параллельных прямых используют символ «». То есть, если прямые а и b параллельны, то можно кратко записать а b .

Обратите внимание: если прямые a и b параллельны, то можно сказать, что прямая a параллельна прямой b , а также, что прямая b параллельна прямой a .

Озвучим утверждение, которое играет важную роль при изучении параллельных прямых на плоскости: через точку, не лежащую на данной прямой, проходит единственная прямая, параллельная данной. Это утверждение принимается как факт (оно не может быть доказано на основе известных аксиом планиметрии), и оно называется аксиомой параллельных прямых.

Для случая в пространстве справедлива теорема: через любую точку пространства, не лежащую на заданной прямой, проходит единственная прямая, параллельная данной. Эта теорема легко доказывается с помощью приведенной выше аксиомы параллельных прямых (ее доказательство Вы можете найти в учебнике геометрии 10-11 класс, который указан в конце статьи в списке литературы).

Параллельность прямых - признаки и условия параллельности.

Признаком параллельности прямых является достаточное условие параллельности прямых, то есть, такое условие, выполнение которого гарантирует параллельность прямых. Иными словами, выполнение этого условия достаточно для того, чтобы констатировать факт параллельности прямых.

Также существуют необходимые и достаточные условия параллельности прямых на плоскости и в трехмерном пространстве.

Поясним смысл фразы «необходимое и достаточное условие параллельности прямых».

С достаточным условием параллельности прямых мы уже разобрались. А что же такое «необходимое условие параллельности прямых»? По названию «необходимое» понятно, что выполнение этого условия необходимо для параллельности прямых. Иными словами, если необходимое условие параллельности прямых не выполнено, то прямые не параллельны. Таким образом, необходимое и достаточное условие параллельности прямых – это условие, выполнение которого как необходимо, так и достаточно для параллельности прямых. То есть, с одной стороны это признак параллельности прямых, а с другой стороны – это свойство, которым обладают параллельные прямые.

Прежде чем сформулировать необходимое и достаточное условие параллельности прямых, целесообразно напомнить несколько вспомогательных определений.

Секущая прямая – это прямая, которая пересекает каждую из двух заданных несовпадающих прямых.

При пересечении двух прямых секущей образуются восемь неразвернутых . В формулировке необходимого и достаточного условия параллельности прямых участвуют так называемые накрест лежащие, соответственные и односторонние углы . Покажем их на чертеже.

Теорема.

Если две прямые на плоскости пересечены секущей, то для их параллельности необходимо и достаточно, чтобы накрест лежащие углы были равны, или соответственные углы были равны, или сумма односторонних углов равнялась 180 градусам.

Покажем графическую иллюстрацию этого необходимого и достаточного условия параллельности прямых на плоскости.

Доказательства этих условий параллельности прямых Вы можете найти в учебниках геометрии за 7 -9 классы.

Заметим, что эти условия можно использовать и в трехмерном пространстве – главное, чтобы две прямые и секущая лежали в одной плоскости.

Приведем еще несколько теорем, которые часто используются при доказательстве параллельности прямых.

Теорема.

Если две прямые на плоскости параллельны третьей прямой, то они параллельны. Доказательство этого признака следует из аксиомы параллельных прямых.

Существует аналогичное условие параллельности прямых в трехмерном пространстве.

Теорема.

Если две прямые в пространстве параллельны третьей прямой, то они параллельны. Доказательство этого признака рассматривается на уроках геометрии в 10 классе.

Проиллюстрируем озвученные теоремы.

Приведем еще одну теорему, позволяющую доказывать параллельность прямых на плоскости.

Теорема.

Если две прямые на плоскости перпендикулярны к третьей прямой, то они параллельны.

Существует аналогичная теорема для прямых в пространстве.

Теорема.

Если две прямые в трехмерном пространстве перпендикулярны к одной плоскости, то они параллельны.

Изобразим рисунки, соответствующие этим теоремам.

Все сформулированные выше теоремы, признаки и необходимые и достаточные условия прекрасно подходят для доказательства параллельности прямых методами геометрии. То есть, чтобы доказать параллельность двух заданных прямых нужно показать, что они параллельны третьей прямой, или показать равенство накрест лежащих углов и т.п. Множество подобных задач решается на уроках геометрии в средней школе. Однако следует отметить, что во многих случаях удобно пользоваться методом координат для доказательства параллельности прямых на плоскости или в трехмерном пространстве. Сформулируем необходимые и достаточные условия параллельности прямых, которые заданы в прямоугольной системе координат.

Параллельность прямых в прямоугольной системе координат.

В этом пункте статьи мы сформулируем необходимые и достаточные условия параллельности прямых в прямоугольной системе координат в зависимости от вида уравнений, определяющих эти прямые, а также приведем подробные решения характерных задач.

Начнем с условия параллельности двух прямых на плоскости в прямоугольной системе координат Oxy . В основе его доказательства лежит определение направляющего вектора прямой и определение нормального вектора прямой на плоскости.

Теорема.

Для параллельности двух несовпадающих прямых на плоскости необходимо и достаточно, чтобы направляющие векторы этих прямых были коллинеарны, или нормальные векторы этих прямых были коллинеарны, или направляющий вектор одной прямой был перпендикулярен нормальному вектору второй прямой.

Очевидно, условие параллельности двух прямых на плоскости сводится к (направляющих векторов прямых или нормальных векторов прямых) или к (направляющего вектора одной прямой и нормального вектора второй прямой). Таким образом, если и - направляющие векторы прямых a и b , а и - нормальные векторы прямых a и b соответственно, то необходимое и достаточное условие параллельности прямых а и b запишется как , или , или , где t - некоторое действительное число. В свою очередь координаты направляющих и (или) нормальных векторов прямых a и b находятся по известным уравнениям прямых.

В частности, если прямую a в прямоугольной системе координат Oxy на плоскости задает общее уравнение прямой вида , а прямую b - , то нормальные векторы этих прямых имеют координаты и соответственно, а условие параллельности прямых a и b запишется как .

Если прямой a соответствует уравнение прямой с угловым коэффициентом вида , а прямой b - , то нормальные векторы этих прямых имеют координаты и , а условие параллельности этих прямых примет вид . Следовательно, если прямые на плоскости в прямоугольной системе координат параллельны и могут быть заданы уравнениями прямых с угловыми коэффициентами, то угловые коэффициенты прямых будут равны. И обратно: если несовпадающие прямые на плоскости в прямоугольной системе координат могут быть заданы уравнениями прямой с равными угловыми коэффициентами, то такие прямые параллельны.

Если прямую a и прямую b в прямоугольной системе координат определяют канонические уравнения прямой на плоскости вида и , или параметрические уравнения прямой на плоскости вида и соответственно, то направляющие векторы этих прямых имеют координаты и , а условие параллельности прямых a и b записывается как .

Разберем решения нескольких примеров.

Пример.

Параллельны ли прямые и ?

Решение.

Перепишем уравнение прямой в отрезках в виде общего уравнения прямой: . Теперь видно, что - нормальный вектор прямой , а - нормальный вектор прямой . Эти векторы не коллинеарны, так как не существует такого действительного числа t , для которого верно равенство (). Следовательно, не выполняется необходимое и достаточное условие параллельности прямых на плоскости, поэтому, заданные прямые не параллельны.

Ответ:

Нет, прямые не параллельны.

Пример.

Являются ли прямые и параллельными?

Решение.

Приведем каноническое уравнение прямой к уравнению прямой с угловым коэффициентом: . Очевидно, что уравнения прямых и не одинаковые (в этом случае заданные прямые были бы совпадающими) и угловые коэффициенты прямых равны, следовательно, исходные прямые параллельны.